万物皆数,自然界不同层次事物的演变生死及相互关联,选用复数进行描述不仅简洁而且自然。比如同时包含电阻
r与电感
l或电容
c的交流电路中(驱动角频率设为
ω),电流波形与电压波形之间的换算不用针对
l或
c进行复杂的微积分运算,只需通过虚数单位
j (电工学中的习惯,以区分电流标识,实际上跟数学中公知的虚数单位 i 等同),就可以将 j
ωl 与
r 复合加减成复阻抗或将 j
ωc 与 1/
r 复合加减成复导纳,而阻抗与导纳的计算,除了运算规则复数化,跟电阻与电导操作一样,利用串并联等规则分析计算没有差异。为什么虚数单位的引入如此神奇地将复杂电路问题化繁为简?我们所享受的这种简洁与便利是怎样被发展(注1)出来的?如此美妙的纯粹的数学跟现实物理世界的对应关系是怎样建立的?如此神奇的刻画世界理解世界的工具对于普通人的生活有没有什么启示性的联系?这些问题实际上也是笔者多年来在复数测量相关的职业工作与对生活不停地观察和思考的对象。碰巧在2019年儿童节那天,给一位受人尊敬的仪器维修工程师70岁寿辰庆祝,会议上笔者对自己关于复数和复数测量学问做了口头的总结交流。本文是文字版总结。以下各章分别对这些问题进行分析讨论。因为主要内容是笔者思考总结所原创的文字,本文跟复数教科书之间的关系希望是:看完此文想再学复数,学过复数欲回看此文。
图1 从自然数到复数的逐步延拓过程图示
经过了零、负数和无理数的引入,人类对数的认识从自然数逐渐延拓发展到实数,基本完成了数轴上的点和对自然数进行有限或无限次加减乘除组合运算结果之间的完整且不重复的对应关系,然而,在求解二次或三次方程根等问题的道路上,随着负数的平方根并不对应某个实数这个新情况,一开始被人们当做不自然的东西直接抛弃不管,现在看来是实数存在开方运算不能自我封闭的缺陷,后来通过对-1平方根(通常被记作 i)为虚数单位的重新定义,将数的概念从基本实数拓展到一实一虚的数对构成的复数,终于完成了加减乘除乘方开方及其有限与无限混合运算结果的封闭定义。关于数的概念逐步扩展,汇总如图1所示,其中列出人类对数的概念认知具有里程碑意义的几个特殊数,包括 1、0、-1、π、e及刚提到的 i。对圆周率π很多人从小学就开始接触,故耳熟能详到小数点后 6 位以上无需再解释。而自然底数e=2.71828…为什么特殊,稍微提一下,这在于以它为底的指数函数y =ex在任意点x*的变化率或斜率与函数曲线从负无穷到x*覆盖的区间面积数值相等,而且都等于该点函数值
y *=e
x *=
y ′*=
y * (
y′ *与
y *分别表示
y 的微分与不定积分函数在
x* 点的数值)。大数学家欧拉发现,e 还有一个神奇之处在于以 i
θ 作为指数时,能实现指数运算跟正弦余弦三角函数运算之间的转换,e
iθ=cos
θ isin
θ,这对于复数的乘除与开方运算简直如虎添翼,不仅根治了复数运算复杂的毛病,而且在有些时候能帮助实代数运算化繁为简(感兴趣的读者可以搜索利用棣莫弗公式证明复杂多倍角正余弦三角函数公式)。一般意义上的复数的实部 虚部、与幅值与幅角表达的含义及其转换关系如图 2 所示。值得一提的是,当
θ=
π时,我们能获得大多数同行都认可、在人类历史上最优美同时内涵最丰富且高度概括了人类智慧的一个数学公式e
iπ 1=0。
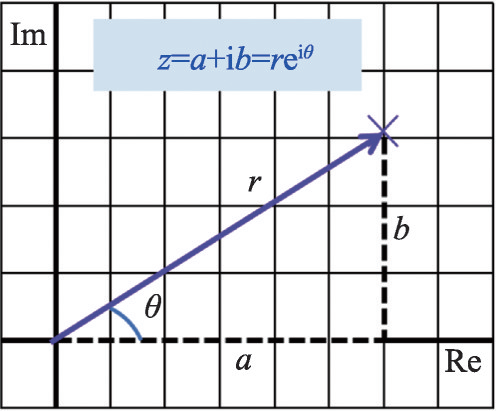
图2 复数构成的代数与几何图示
复数的加法与指数表达之间的等效换算关系如图 3 所示,关于更多更全面的复数计算及复变函数介绍请参考专门的复数教科书
[1],在这里需要指出的一点是,有些作者可能是图省事,在实部虚部求幅角的时候简单但错误地表达成
b/
a 的反正切,这种简单不仅错在
a 的数值为0时非常尴尬,更在于反正切的函数范围只在第一与第四象限,当复数位于第二或第三象限时将不可避免地出现往第一第四象限折叠的问题。正确的做法是对实部、虚部的符号做分类处理,即需要双参数输入函数,在多种编程语言中已经有现成的函数模块可供调用,比如脚本语言中一般支持 atan2 函数,它支持双参数输入并能输出完整四象限角度,图形语言比如 labview中直接有实部虚部到幅度幅角的转换函数。还有一点值得一提,虽然实部虚部与极坐标表示之间能够相互换算,但严格来讲二者并不完全等价。关键在原点处,实部虚部定义0 i0很自然,不过极坐标表示就没有确定的相位角,尽管编程语言中通常将原点的相位角置零,运用的人要清楚这个细微但却是本质的差异。不管怎样,读者看过本文以后如再碰到文章或教科书中直接将
b/
a 的反正切作为复数的相位角,完全有理由直接怀疑其作者对复数的理解与认知水平。
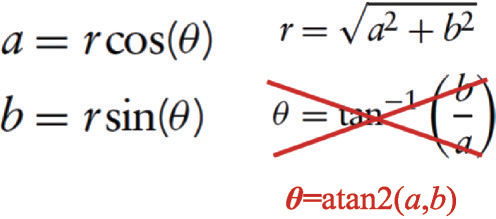
图 3 复数的两种基本表示方法之间的等价换算
实数运算拓展到复数运算因为产生新的现象,不能完全受实数运算中的规则束缚,有些在实数中的常识,在复数运算处理时可能并不适用要引起注意,这里举例讲复数乘方运算中的一条反常识之处:复数乘方运算稍不注意就会引起自相矛盾的悖论,如图4所示,据记载最初由放牛娃出身的克劳森(thomasclausen)于1827年提出
[2]。克劳森悖论实际上不是复数的问题,而是在复数乘方运算过程中,复底数的相位求取是多值化的,跟乘方运算的指数相乘的相位应当为相位主值加上2
πk (
k 为整数)。如图5所示的两个乘方运算结果举例,i
i 等于一系列实数,其中
k=0时相位主值对应的值为 e
(- π/2),一个约等于0.2的无理数;另一个例子,1
i 根据实数乘方运算常识,1的所有次方总等于1,但这里1只是其结果之一,因为 1
i 除了在
k=0时等于1以外,还对应其他无穷个结果。当然,复数运算中也有人类迄今尚未理解的难题,比如让人着迷却仍然不得其解的黎曼猜想,由于已经超过本文的讨论范围,感兴趣的读者请自己去检索。
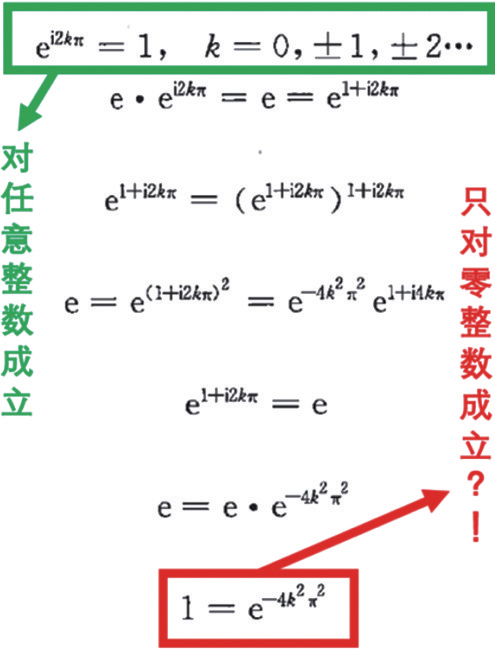
图4 克劳森提出的复指数悖论问题
[2]
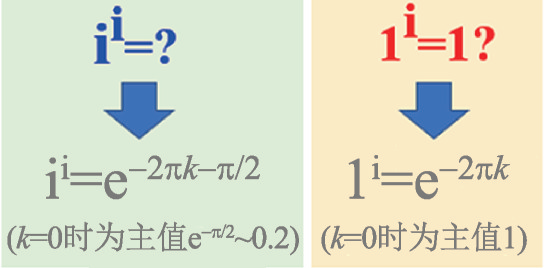
图5 虚指数的多值性示例
至此,复数的基本概念及运算规则已经介绍结束。然而,不得不承认,复数是怎样被发展出来的,前面的介绍只是过于简单的版本,跟真实的人类认识与应用复数的历史出入比较大,如果要我对于历史这段不严谨的介绍给一个借口,那无非是为了节约读者的宝贵时间,而且这个介绍丝毫不影响复数是什么这一知识的获取。如果只重知识,不管真实,可以跳过本段去直接阅读下一章。但凡是对真实有点兴趣的读者,建议耐心看完本段文字与汇总本段的图6。笔者认为,知道真实的知识产生的过程,不仅仅能让我们珍惜自己轻松就学到的知识,也让我们意识到我们学到的知识并非人类知识的终点,进而让自己的内心被薪火相传,并获得进一步去创新从而延伸人类知识的动力。如图6所示,这是一个以千年的 时 间 尺 度 通 过 关 键 事 件 节 点 (what/when/who) 依次串联来描述我们人类认识与应用复数的过程,事件涉及到的时间与人物的原始数据部分来源于nahin博士的书与数学手册
[2,3],为了读者能更好地理解这个进展过程,笔者将这些事件分成几类进行介绍:
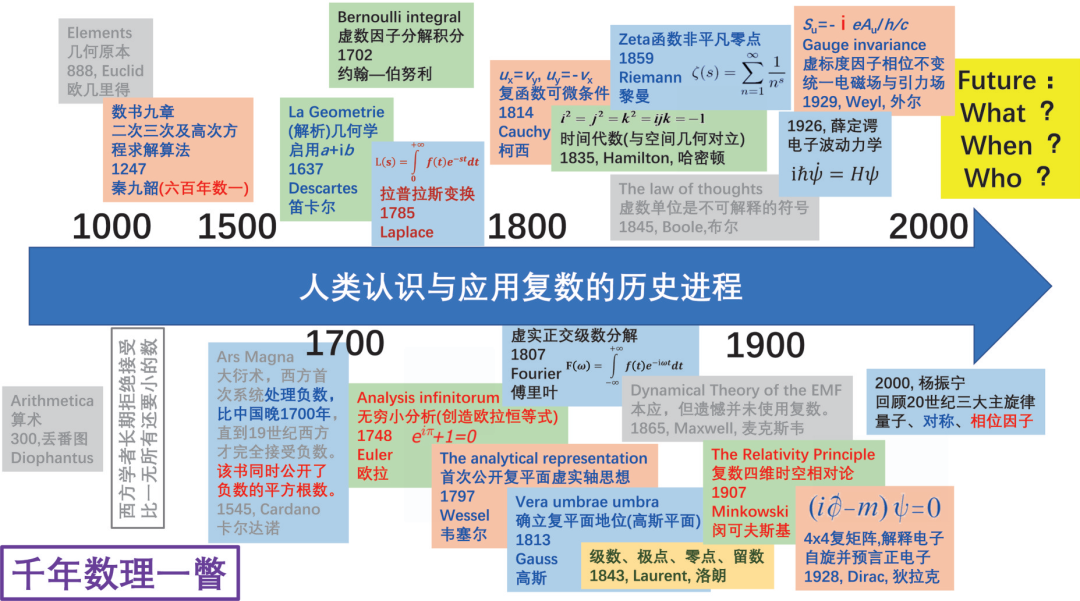
图6 以千年尺度汇总显示人类认识与应用复数的历史进程
(1) 奠基
复数的最初渊源从代数与几何的方向分别可追溯到公元300年由丢番图(diophantus)整理编写的《arithmetica》(算术),与公元888年由欧几里得 (euclid) 编写的《elements》(几何原本)。
(2) 铺垫
1545年卡尔达诺 (cardano) 在《ars magna》(大衍术)中系统进行了负数及运算的论述,首次公开负数的平方根数的概念;1637年笛卡尔(descartes)在《la geometrie》(几何学)中公开了
a i
b 解析法处理复数;韦塞尔(wessel)于1797年公开虚实轴组成复平面处理矢量的思想;柯西(cauchy)在1814年公开复函数可微条件,拉开了复变函数的微积分学;洛朗(laurent)于1843年公开了复变函数独有的一套级数思想与零点和极点处理方法,引入留数(洛朗级数的一次倒数项系数);1807 年傅里叶(fourier)公开倍频但幅度稳定的正弦余弦分别作为虚部实部的级数来进行函数的分解;1785年拉普拉斯(laplace)引入一套复指数变换方法,研究失稳过程有时非它不可。
(3) 点睛
前面提过的欧拉恒等式由欧拉(euler)在1748年公开证明,没有欧拉,这个恒等式也许会被引入,但不知道要迟多少年;一向谨慎低调的数学王子高斯(gauss)在1813年终于公开确立复平面的历史地位,复数的全面推广从此正式开始;闵可夫斯基(minkowski)于1907年公布通过虚数单位和光速跟时间相乘,三维空间复合,引入四维时空,证明了时空相对变化中的绝对不变;薛定谔(schrödinger)在1926年提出闻名于世的电子波动力学方程,尽管原文
phys. rev., 28, 1049(1926)中没有直白地写出他去世后在墓碑上刻着带虚数单位模样的方程(如图6中1926年事件块中所列),但在原文第9部分对含时波函数中出现虚数单位与相位±2
πet/
h,足够表达波函数在特定能量下的振荡性质,并启发后人理解量子力学的奥妙。
(4) 发扬
首先不得不提黎曼(riemann),尽管40岁就英年早逝,但在他短暂的一生中,除了前面提到的黎曼猜想,他与柯西一样都对复分析作出了重要贡献,而且比柯西更加富有创造性地从微分几何角度开展复分析,并首次往人类数理知识库中引入非欧几何,这对20世纪广义相对论与弦论的诞生提供了良好的铺垫。
狄拉克(dirac)对量子力学波函数进行了相对论性改造,其中关键的一步是将哈密顿算符变成4×4的复矩阵,利用矩阵具有反对易性质调和了时间与空间平方反对称与一阶微分对等之间的矛盾,让经过改造后的波函数的第四分量非常好地对应解释电子1/2自旋,并预言了正电子的存在,极大地推动了量子力学的发展。
外尔(weyl)在统一电磁场与引力场,构建伟大的规范不变理论的过程中,至关重要的一步是,找到跟电荷守恒相对应的对称性是复波函数的相位不变性,该相位不变规律在电磁学中可以推导出麦克斯韦方程组,是电磁相互作用理论的终极基石。
杨振宁(c. n. yang)经过艰苦卓绝的群论推演,用2×2复矩阵找到质子与中子之间的同位旋对称,后来盖尔曼(murray gell-mann)经过3×3的复矩阵运算进一步获知微观世界基本粒子的构建规则,从而准确解释或预测出全部微观基本粒子的种类及相互作用,杨先生与盖尔曼引入被称为标准模型的理论实现了除引力外所有已知基本力的伟大统一。顺便一提,在2000年杨先生回顾20世纪物理学三大主旋律为:量子、对称、相位因子。
(5) 遗憾
在复数的发展过程中,从二元复数到多元复矩阵的过程中,代数学上还经历过三元数、四元数、乃至八元数的尝试,其中最著名的要数哈密顿(hamilton)创立的四元数(quaternion),遗憾的是,多元复数的代数运算简洁程度与效果比不上2×2与4×4复矩阵,从而在20世纪物理学发展的大舞台上并没有获得哈密顿本人预期的实用,尽管在比较小的学科分支上也有独到的应用,比如将四元数的模设成1时可以用于描述三维空间旋转,空间导航时相比通常的欧拉角方法有更小的误差与较高稳定性。当然,形式上将 lijk 换成2×2复矩阵组并不影响实质上的大同小异,从这个意义上讲,形式上未被重视不应该掩盖哈密顿的超复数思想与逻辑的伟大。
除此以外,19世纪中叶,复数的概念已经被数学主流认可并应用的时候,逻辑代数创始人布尔(boole)却坚持认为虚数单位是不可解释的符号,现在看来让人难以理解,不过二值比特逻辑有其自身的优势及发展之路,虚数在数值逻辑中的确不必要,或许在未来某天模拟计算与数值计算平分秋色之时,复数在计算机架构中的重要性将不言而喻。
还有,麦克斯韦(maxwell)在他1865年“a dynamic-al theory of theelectromagnetic field”论文中,未见使用虚数,子方程数达20个之多, 后来多亏oliver heaviside与willard gibbs运用矢量分析进行大幅度改造才使得麦克斯韦方程组成型到容易理解的闻名于世的四个子方程形式,当然瑕不掩瑜,麦克斯韦的这篇论文在电磁规律综合并牢固确立场的概念、引入位移电流、同时通过波速证明电磁波是光这几个方面的贡献是划时代的。
(6) 插曲
我们知道,负数是虚数之源,虚数的引入必须以负数为前提,但不知因何原因,在古代中国引入并运用负数非常自然,而西方正式接受负数比中国晚约1700年,不过西方在接受负数后随即就开启了虚数的研究,而中国人对虚数的发展未见任何实质性的贡献,只是由《数书九章》中秦九韶提出的二次、三次及高次方程求解算法,可见他是中国古人中距离虚数发现最近的人,而且更加难能可贵的是,《数书九章》是《几何原本》与《大衍术》之间约600年间地球上数一的数学著作。
还有一则,在欧拉恒等式被引入之前,复数的计算通常需要高超的数学技巧,比如约翰·伯努利运用(
x i)(
x-i)=1
x 2 的技巧找到了反正切与对数函数之间的内在联系,并运用于虚数因子分解积分,被莱布尼茨(leibniz)评价为非凡智能的一个优美神奇。
(7) 可期
跟其他人类知识体系一样,复数发展至今不应是终点,未来有更重要的发展事件也是可期的。我们知道以复数波函数为主要特征的量子力学样样都好,屡次都被证明是正确的,至今也还没有发现被实验结果证否的事件,但就是推不出引力方程,让人隐忧哪里有些不对,实现大统一或证明大统一是不可能实现的幻想的突破性的事件,让我们努力使它在我们有生之年发生。
尽管复数及其重要性广为人知,但也不可否认,复数测量长期以来只是一个小众的主题,笔者曾经在南京大学一个网络课程中听主讲老师竟随口说出一句复数还不能被测量,也许该老师的表述有笔者没有留意到的小语境,但侧面反映出了解复数测量的群体远小于了解复数的群体这个事实。还有很多同行每天都在使用在信号或波函数层次实质上都是复数测量的仪器,比如频谱仪、阻抗分析仪、介电分析仪、矢量网络分析仪、交流磁化率仪、交流电压表等等,但由于被测物理量或仪器名称上不容易看出是在进行复数测量,导致复数测量本身很少被人关注。
真实世界中的复数测量通常不是直接有一副如图2一样的抽象坐标轴平面让人用尺去度量,而是隐藏在变化的波函数中,比如随时间变化的交流信号或随空间变化而起伏的波形,时域的频率或空域的波数可以千差万别,对应的复数测量实部虚部结果也许会一样,但这两个复数在物理世界能相提并论的前提条件必须是“在同一条船上”,这个话题将在下一章展开讨论。
与其他测量手段需要诸如光子、电子、中子等探针才能看到跟探针相当的结构信息类似,复数测量波函数一般也使用复数“探针”,一个跟被测波函数步调一致的参考波函数,如图7所示参考信号被稳频后的正弦信号所承载。为了同时获得实部与虚部,参考信号通过相位稳定部件分成相位差成对锁定成90°的在蓝线中的余弦信号与浅蓝色的正弦信号,它们分别通过相敏检波部件,实际上是二入一出的乘法部件,跟红色标识的需要测量信号分别相乘后输出经过低通滤波获得的被测信号跟参考信号频点
ω0一致的实部与虚部,分别如绿色与浅绿色线所示,从而完成复数测量过程。在信号强度不够的情况下,当然还可以选取辅助的前端或后置放大。由傅里叶级数规则,同频的正弦与余弦信号正交(正交意味着二者经过乘法和低通滤波部件后的输出为零),于是实部和虚部测量结果之间在原理上保持相互独立,同时被测信号中所有
ω0的 2、3、4……倍频率的正弦与余弦分量跟前述
ω0频点的正弦与余弦之间彼此正交,故而复数的整个测量过程实质上是一个只检出
ω0频点实部与虚部的窄带滤波过程,其他频段信号自动被作为干扰消除。
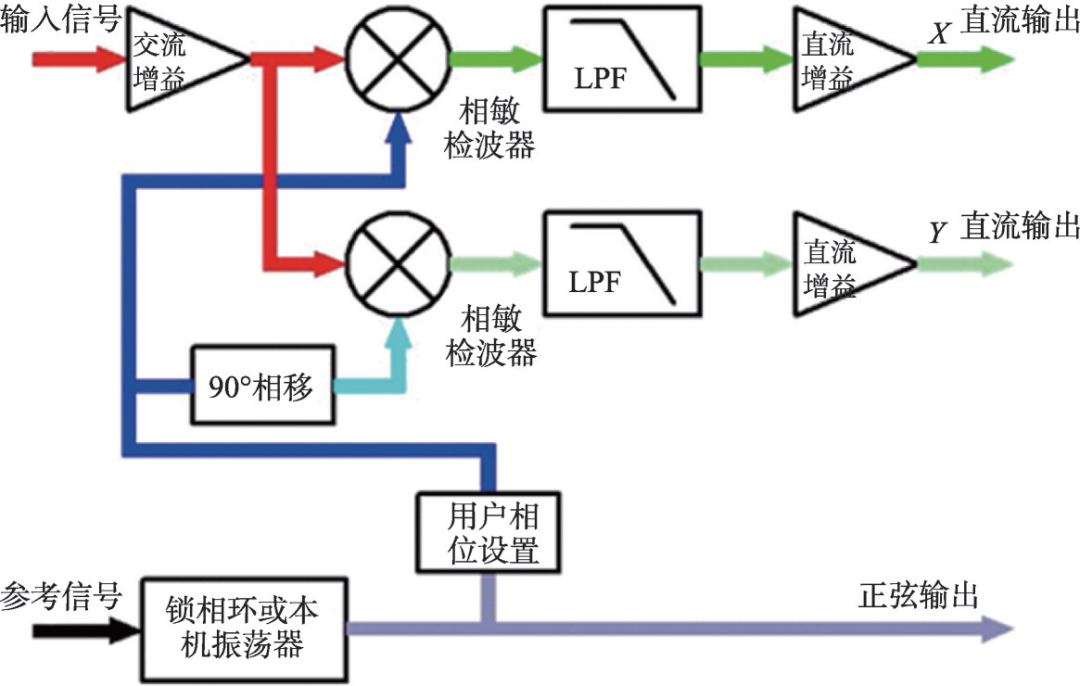
图7 锁相放大器测量原理示意图
[4]
由测量原理看出
ω0频点的稳定极为重要,在普通的振荡源的频率稳定性不够的时候,需要增加锁相环(phase lock loop,pll)部件,其结构如图8所示,在强制外部参考的模式下,受控振荡源为了和外部频点保持一致,需要实时测量跟外部参考信号的相位差并进行自我调整,通过相位差的锁定来维持测量频点的稳定。因而这种复数测量方法与工具通常被称之为锁相技术与锁相放大器(lock in amplifiers)。
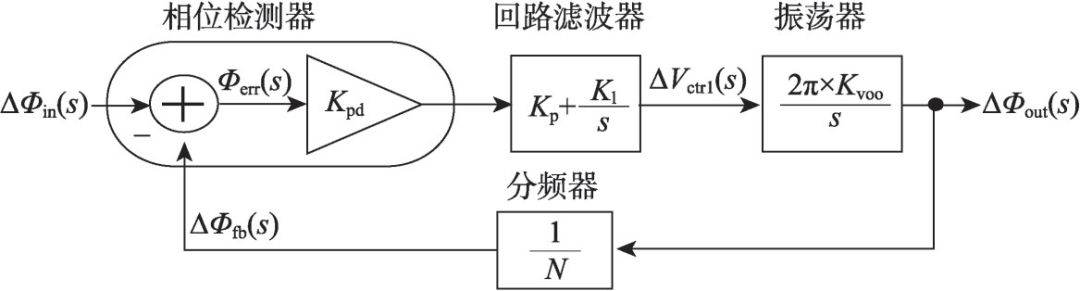
图8 锁相环结构图示
[4]
如此可见,用锁相技术实现复数测量的关键在于交流变化维度的锁相环跟踪与实部虚部的正交相敏检波测量,更多的专业介绍请参考文献
[4]。这里对锁相的含义,为让外行人能更好理解这个复数测量的强大工具,做一点延伸解读:锁相,跟成语相夫教子中的作为动词的“相”含义默契,夫妇之间的关系实际上是一个长期的相位和步调通过锁定达到美满的境界,如果失锁就比较麻烦了。此外,锁相环这种自动保持稳定步调但又具备一定的随外界环境而自我调节能力的神奇部件,何尝不是一个原始态的机器心灵?
15年前,当我第一次因为弱磁电耦合测量需要开始接触到锁相放大器的时候,实验室有一台老旧的手动设置纸笔记录的eg&g parc model 124a from princeton applied research,边看波形边扫频并用纸笔boring的记录锁相测量结果的时候,不知怎么就冒出一个idea,有波形数据(当时国产数字存储示波器已经问世,我恰巧就购买了现在早已停产属于普源rigol ds5062c这个国产骨灰级数字存储示波器),我可以在电脑里完成锁相啊,完全取代普林斯顿的eg&g 124a的功能,干嘛要多此一举费力还容易出错地将精力白白耗在古董锁相上?有想法的时候通常自动具备不停的干劲,几个月下来,经过dll的c调用驱动接口、自学虚拟仪器labview图形语言、vi实施锁相算法、自动测量程序控制一路逐层通关,竟然将最初设想的功能实现了,而且锁相性能与测量效率都有明显提升(性能与效率对比后来投稿发表在
meas. sci. technol. 上
[5]),自此终于彻底废弃了普林斯顿的eg&g 124a,我也从枯燥的手摁笔录工作中解放出来。用国产几千元人民币的低端示波器,加上自己编写的虚拟仪器算法,完美取代从普林斯顿进口的几千美元的锁相,让我领悟到示波器使用的 “ 看 ”、“ 测 ”、“变”、“ 驯 ”四重境界,并网络公开分享
[6,7]。对自己辛苦编写的代码也毫无保留地在网络上公开
[8],公开代码行为我认为是自信开放地将过去的成就放下,积极采取面向未来继续创新的姿态。除此以外,这个经历对于训练我养成奋斗者思维的帮助很大,后来的工作中在面临资源不足的困难时,从不想着抱怨,只一味主动激励自己积极行动将困难当作提升能力的机遇。

图9 频率、幅度和相位之间一体性关系的图示
上段介绍笔者进入复数测量研究生涯的起点,这个起步经历只是验证锁相可以被虚拟仪器化,并无原理创新,接下来进入正题,鸟瞰笔者这些年在复数测量原理创新方面取得的一点点进步上[9-11]。上一章谈到,用锁相进行复数测量的两大关键,锁相环频率跟踪与虚实部相敏检波,而且传统方法测量结果是跟参考信号频率对应的复数,被测复数真实的交变频率是作为隐变量,通常被当作跟参考频率完全一致。然而被测信号的频率与参考信号的频率总能完全一致吗?这个问题是笔者在想尽办法改进锁相时的关键切入点,答案显然是否定的,让两路信号保持频率一致在一致度要求不高(比如0.1%)时不难,但要达到 1ppm 量级的不一致度时就很不容易,由图8可知,锁相只在参考信号一侧应用了锁相环保证频率稳定,而另一端,恰好是被测信号通常无法稳频,此时由于介质非线性、传输色散、多普勒效应等不可避免引入频漂,频漂的存在,造成相敏检波的两个输入信号存在频差,一定会导致实部虚部测量结果的不准乃至错误,因为信号频率与幅值及相位共同描述一个完整的信号,分别好比浮在水面上的船体与船帆的位置及方向,如图9所示,以船体作参照物看船帆相对固定,而以岸作为参照物时则在波浪中更多看到的是船帆的飘摇,因而固定参考信号的锁相工作像是现代版的刻舟求剑。
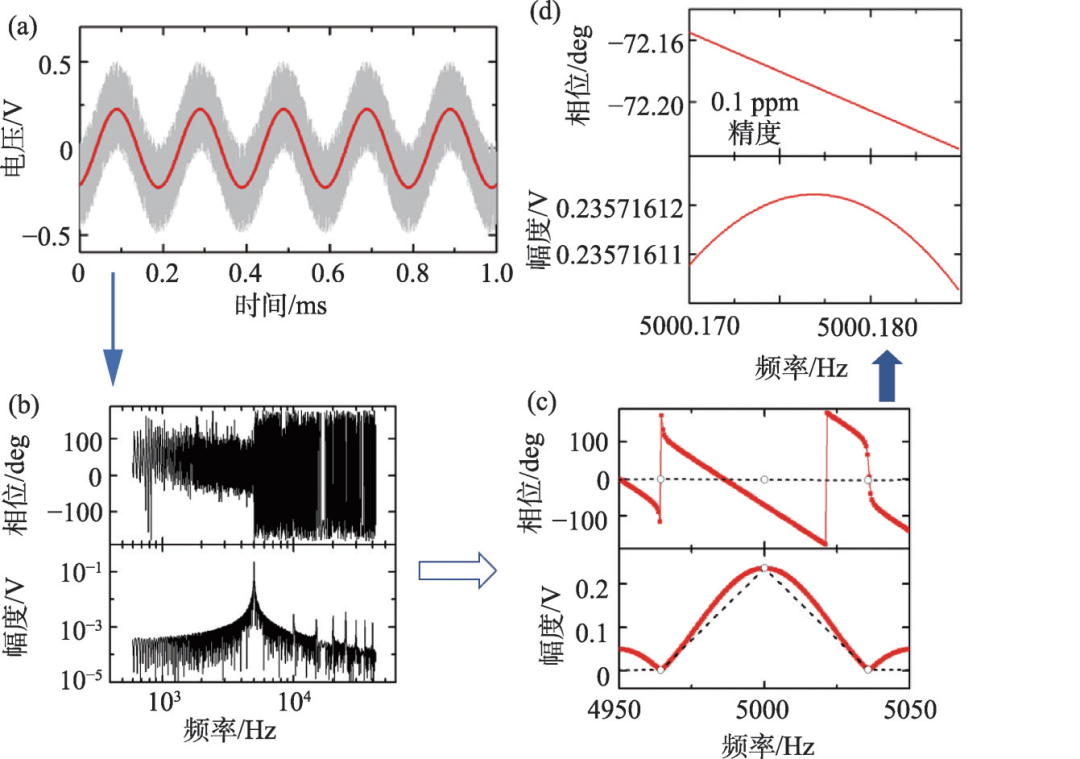 图11 锁相频率计与快速傅里叶变换(fft)的测频精度比较笔者解决这个问题的思路如图10所示,实际上是取消被测信号的频率与参考信号的频率一致的假定,通过锁相的算法改进成频率的泛函,同时解决被测信号的抗噪测频与准确锁相两个问题,新方法的名称叫测频锁相仪或锁相频率计。使用锁相频率计的测频精度跟快速傅里叶变换(fft)的对比效果如图11所示,我们知道傅里叶变换的频率精度受取样窗口的制约,很难进一步提高,而锁相频率计新方法能够在频域进行超精细扫描,比如图11中相比fft的测频精准度只有约万分之一,锁相频率计能精细到百万分之一以内。当然,精度的提高在原理上有限度,一定的时间长度与采样率条件下频率测量不确定性存在统计学上的下限即cramer-rao下限[10,12],经过数值仿真可知,新方法在不同信噪比条件下的测频精度接近理论下限,如图12所示。近期,笔者理论推导出单周期信号的锁相频谱在估计频点附近的局部函数形式,证明了正确的函数形式优于经验的抛物线,并基于此使用较少的计算量就能达到精确测频的结果,当数字处理信号长度为n 时,相比fft的复杂度o(n *logn),新算法的复杂度减为o(n)[10,11]。通过高速ad与fpga芯片组合搭载新算法形成的样机,对某977hz信号的实测结果如图13所示,实际测频不确定度约±0.15ppm。为了获得横向对比,2019年初样机在中山大学锁相实验室进行了第三方对比测试,结果显示锁相性能的两个核心指标,测频精度与噪音谱密度,在时间常数1s时,基于新原理的锁相样机分别为
图11 锁相频率计与快速傅里叶变换(fft)的测频精度比较笔者解决这个问题的思路如图10所示,实际上是取消被测信号的频率与参考信号的频率一致的假定,通过锁相的算法改进成频率的泛函,同时解决被测信号的抗噪测频与准确锁相两个问题,新方法的名称叫测频锁相仪或锁相频率计。使用锁相频率计的测频精度跟快速傅里叶变换(fft)的对比效果如图11所示,我们知道傅里叶变换的频率精度受取样窗口的制约,很难进一步提高,而锁相频率计新方法能够在频域进行超精细扫描,比如图11中相比fft的测频精准度只有约万分之一,锁相频率计能精细到百万分之一以内。当然,精度的提高在原理上有限度,一定的时间长度与采样率条件下频率测量不确定性存在统计学上的下限即cramer-rao下限[10,12],经过数值仿真可知,新方法在不同信噪比条件下的测频精度接近理论下限,如图12所示。近期,笔者理论推导出单周期信号的锁相频谱在估计频点附近的局部函数形式,证明了正确的函数形式优于经验的抛物线,并基于此使用较少的计算量就能达到精确测频的结果,当数字处理信号长度为n 时,相比fft的复杂度o(n *logn),新算法的复杂度减为o(n)[10,11]。通过高速ad与fpga芯片组合搭载新算法形成的样机,对某977hz信号的实测结果如图13所示,实际测频不确定度约±0.15ppm。为了获得横向对比,2019年初样机在中山大学锁相实验室进行了第三方对比测试,结果显示锁相性能的两个核心指标,测频精度与噪音谱密度,在时间常数1s时,基于新原理的锁相样机分别为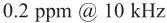 与
与 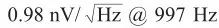 ,相同条件下对照的瑞士苏黎世仪器hf2li 的与美国斯坦福仪器sr865的测频精度是
,相同条件下对照的瑞士苏黎世仪器hf2li 的与美国斯坦福仪器sr865的测频精度是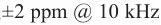 ,这两台仪器噪音谱密度则分别是
,这两台仪器噪音谱密度则分别是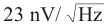 与
与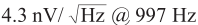 ,对比数据可见,在这两个指标上笔者研发的样机性能领先。目前样机正在推向问世与接受小量定制,在高性能测频锁相、小尺寸集成与柔性软硬件定制方面跟同类产品相比具有独创优势,未来若干年将逐步进行市场与技术迭代以实现大批标准化产品定型。
,对比数据可见,在这两个指标上笔者研发的样机性能领先。目前样机正在推向问世与接受小量定制,在高性能测频锁相、小尺寸集成与柔性软硬件定制方面跟同类产品相比具有独创优势,未来若干年将逐步进行市场与技术迭代以实现大批标准化产品定型。
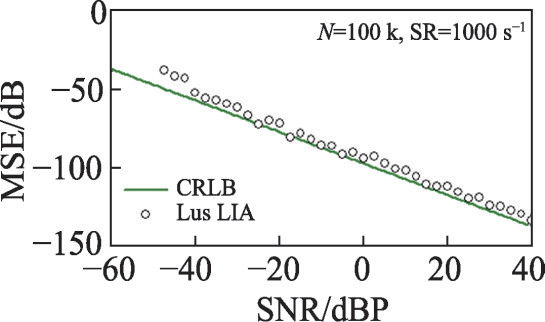 图12 新型锁相频率计在不同信噪比条件下的测频精度与理论极限 cramer-rao lower bound(crlb)对照图
图12 新型锁相频率计在不同信噪比条件下的测频精度与理论极限 cramer-rao lower bound(crlb)对照图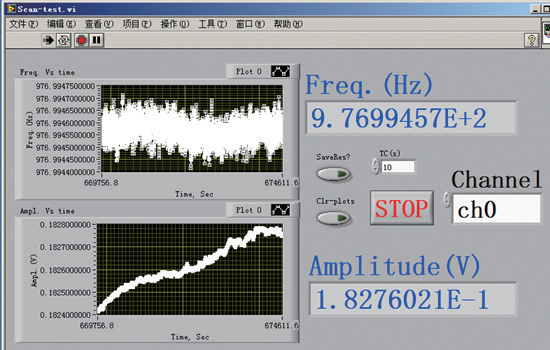 图13 新型锁相频率计对一个977 hz实际信号的测量结果(监控持续约 80分钟)从读研究生时开始接触复数测量于起步时用虚拟仪器在国产低端示波器替代美国普林斯顿的古董锁相,到如今定制芯片硬件中嵌入原理创新的锁相仪器的核心指标超越瑞士苏黎世仪器与美国斯坦福仪器的主流锁相,笔者作为测频锁相奋斗者的时光流逝了15年。
图13 新型锁相频率计对一个977 hz实际信号的测量结果(监控持续约 80分钟)从读研究生时开始接触复数测量于起步时用虚拟仪器在国产低端示波器替代美国普林斯顿的古董锁相,到如今定制芯片硬件中嵌入原理创新的锁相仪器的核心指标超越瑞士苏黎世仪器与美国斯坦福仪器的主流锁相,笔者作为测频锁相奋斗者的时光流逝了15年。
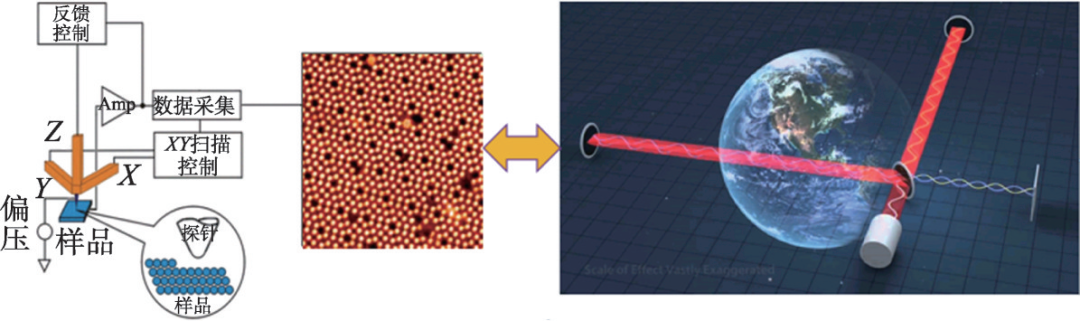 图14 极微观结构与超宏观事件探测都离不开复数测量(显微探针与引力波探测示意图均源自网络)
随着中国智造的加速转型,复数测量的普适度与深度在继续,在人类看得见摸得着的范围内,未来的智能感知、准确定位与互联、精密制造、与痕量物质探测中锁相测量的应用前景让人乐观。在人类肉眼难以感知到的超微观与超宏观世界,如图14所示,亚原子与深太空探索更是无止境,无论浩瀚与微渺,不管刹那还是永恒:复数事件不息,复数测量不止。
图14 极微观结构与超宏观事件探测都离不开复数测量(显微探针与引力波探测示意图均源自网络)
随着中国智造的加速转型,复数测量的普适度与深度在继续,在人类看得见摸得着的范围内,未来的智能感知、准确定位与互联、精密制造、与痕量物质探测中锁相测量的应用前景让人乐观。在人类肉眼难以感知到的超微观与超宏观世界,如图14所示,亚原子与深太空探索更是无止境,无论浩瀚与微渺,不管刹那还是永恒:复数事件不息,复数测量不止。
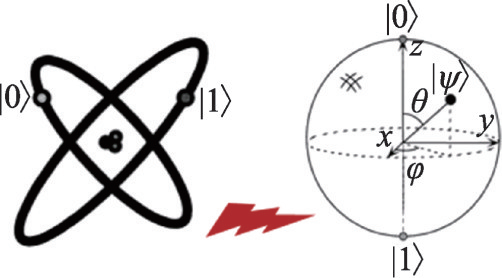 前面在讨论布尔于复数发展过程中的遗憾时,已经提到未来计算机应是模拟计算与数字计算平分秋色,各挥所长。模拟计算中最引人瞩目的应是量子计算,在接近自然的搜寻与大数分解等问题上相比数字计算具有无与伦比的并行加速效率优势。对比当前主流的二值数值比特,量子比特的本质是复数比特[13],如图15所示,以电子|0>与|1>双态轨道举例,双态的混叠可能性在球面上,球面与复平面之间满足相互等效的投影关系(详见附1)。尽管量子计算机中必须使用大量的锁相放大器用于制备量子态与监控量子态的相干性,但复数比特的直接测量依然是个严峻的难题,短期内无法实现,因为量子复数比特中的相位是内在空间的相位,与宏观的波函数中相位完全是两回事,不能生搬硬套,正如狄拉克先生principles of quantum mechanics一书的第一章从哲学高度画出的big与small的界限,在small的世界里,big世界里的概念规则方法必定失效,除非技术的进步能将big与small之间的界限往下挪动一层,比如一定程度上解构量子比特的内在自由度并制备出相应的复数比特探针。从这个角度来看,量子计算机离实用还非常遥远,但这一天终将到来的吸引力如此美好。
前面在讨论布尔于复数发展过程中的遗憾时,已经提到未来计算机应是模拟计算与数字计算平分秋色,各挥所长。模拟计算中最引人瞩目的应是量子计算,在接近自然的搜寻与大数分解等问题上相比数字计算具有无与伦比的并行加速效率优势。对比当前主流的二值数值比特,量子比特的本质是复数比特[13],如图15所示,以电子|0>与|1>双态轨道举例,双态的混叠可能性在球面上,球面与复平面之间满足相互等效的投影关系(详见附1)。尽管量子计算机中必须使用大量的锁相放大器用于制备量子态与监控量子态的相干性,但复数比特的直接测量依然是个严峻的难题,短期内无法实现,因为量子复数比特中的相位是内在空间的相位,与宏观的波函数中相位完全是两回事,不能生搬硬套,正如狄拉克先生principles of quantum mechanics一书的第一章从哲学高度画出的big与small的界限,在small的世界里,big世界里的概念规则方法必定失效,除非技术的进步能将big与small之间的界限往下挪动一层,比如一定程度上解构量子比特的内在自由度并制备出相应的复数比特探针。从这个角度来看,量子计算机离实用还非常遥远,但这一天终将到来的吸引力如此美好。
 从上文可以看出,在人类历史上,复数到很晚才得以发展,甚至直到20世纪才被发现非常有用,当前我们正处在人类运用复数进一步加速提升生产力的时代,锁相技术将会不可避免地被更深入的集成与更广泛地应用。笔者有理由相信,随着电磁学、相对论与量子信息在人类科技文明发展过程中的更全面渗透,掌握并运用复数的人们将能更从容地面对未来的变化与未知的挑战。
复数的内涵对于我们能有什么启示?有一首复数之歌,英文原歌词在本章后面(注2),作者姓甚名谁可惜未被考证,歌词跟《共和国战歌》的调子非常合拍,而且非常准确地道明复数的魅力源于虚数单位,-1的平方根,歌词中被反复咏唱的,the root of minus one,然而,虚数单位的魅力源于什么?what's the root of the root of minus one? 作者通过自己对复数的理解与应用获得的感悟是,i处在正负之间,是相反操作的一半,离开正却未到负,不正不负,像是举棋待定,像是不可捉摸。对于 i 这种独立的自然属性,读者您一定也会若有所思,并会相信个人经历与社会事件除了笼统绝对的黑白与对错之外,在没有完整了解情况前,还有不黑不白不对不错的中庸取向可选,适当跳出自己所处的局部时间与位置,分析手头掌握的可靠信息,实事求是地对已有的一份根据形成对应的一份结论,不是吗?
从复数测量的实质是整体相位准确测量的原理,我们可知局部孤立的事件难以测到复数的相位信 息,从不正不负不黑不白的 i 取向看足够长时间或拉足够远的视角, 一定能更准确地掌握事件整体趋势,并坚定地将自己的思想与行动 跟真实的长远趋势保持一致。碰巧independent与imaginary一样,都以虚数单位 i 开头。正如送给读者的下面四句话:
最后,作者衷心希望您通过本文的阅读,有所思、有所获,更淡定、更快乐。
注 1:关于发明vs发现的用词,数学专家也不一定能作出明确统一的辨析,因为其中涉及到深奥的可能脱离科学可证否性问题的讨论。很多人认同,复数作为解释工具体系,是被发明的;但其中经过人类实践反复证明过的普遍逻辑与理性,说是发现也没有不妥。为了避免这个细节让读者群体取向性分离从而影响主体信息的传达,本文在相关地方使用“引入”或“发展”表达双重含义的叠加效果。
注 2:the complex number song(author: unkown; tune: battle hymn of the republic)
mine eyes have seen the glory of the argand diagram,
they have seen the i's and thetas of de moivre's mighty plan.
now i can find the complex roots with consummate elan,
with the root of minus one.
complex numbers are so easy;
complex numbers are so easy;
complex numbers are so easy;
with the root of minus one.
in cartesian co-ordinates the complex plane is fine,
but the grandeur of the polar form this beauty doth outshine.
you be raising i 40 to the power of 99,
with the root of minus one.
you'll realise your understanding was just second rate,
when you see the power and magic of the complex conjugate.
drawing vectors corresponding to the roots of minus eight,
with the root of minus one.
从上文可以看出,在人类历史上,复数到很晚才得以发展,甚至直到20世纪才被发现非常有用,当前我们正处在人类运用复数进一步加速提升生产力的时代,锁相技术将会不可避免地被更深入的集成与更广泛地应用。笔者有理由相信,随着电磁学、相对论与量子信息在人类科技文明发展过程中的更全面渗透,掌握并运用复数的人们将能更从容地面对未来的变化与未知的挑战。
复数的内涵对于我们能有什么启示?有一首复数之歌,英文原歌词在本章后面(注2),作者姓甚名谁可惜未被考证,歌词跟《共和国战歌》的调子非常合拍,而且非常准确地道明复数的魅力源于虚数单位,-1的平方根,歌词中被反复咏唱的,the root of minus one,然而,虚数单位的魅力源于什么?what's the root of the root of minus one? 作者通过自己对复数的理解与应用获得的感悟是,i处在正负之间,是相反操作的一半,离开正却未到负,不正不负,像是举棋待定,像是不可捉摸。对于 i 这种独立的自然属性,读者您一定也会若有所思,并会相信个人经历与社会事件除了笼统绝对的黑白与对错之外,在没有完整了解情况前,还有不黑不白不对不错的中庸取向可选,适当跳出自己所处的局部时间与位置,分析手头掌握的可靠信息,实事求是地对已有的一份根据形成对应的一份结论,不是吗?
从复数测量的实质是整体相位准确测量的原理,我们可知局部孤立的事件难以测到复数的相位信 息,从不正不负不黑不白的 i 取向看足够长时间或拉足够远的视角, 一定能更准确地掌握事件整体趋势,并坚定地将自己的思想与行动 跟真实的长远趋势保持一致。碰巧independent与imaginary一样,都以虚数单位 i 开头。正如送给读者的下面四句话:
最后,作者衷心希望您通过本文的阅读,有所思、有所获,更淡定、更快乐。
注 1:关于发明vs发现的用词,数学专家也不一定能作出明确统一的辨析,因为其中涉及到深奥的可能脱离科学可证否性问题的讨论。很多人认同,复数作为解释工具体系,是被发明的;但其中经过人类实践反复证明过的普遍逻辑与理性,说是发现也没有不妥。为了避免这个细节让读者群体取向性分离从而影响主体信息的传达,本文在相关地方使用“引入”或“发展”表达双重含义的叠加效果。
注 2:the complex number song(author: unkown; tune: battle hymn of the republic)
mine eyes have seen the glory of the argand diagram,
they have seen the i's and thetas of de moivre's mighty plan.
now i can find the complex roots with consummate elan,
with the root of minus one.
complex numbers are so easy;
complex numbers are so easy;
complex numbers are so easy;
with the root of minus one.
in cartesian co-ordinates the complex plane is fine,
but the grandeur of the polar form this beauty doth outshine.
you be raising i 40 to the power of 99,
with the root of minus one.
you'll realise your understanding was just second rate,
when you see the power and magic of the complex conjugate.
drawing vectors corresponding to the roots of minus eight,
with the root of minus one.
 图2 复数构成的代数与几何图示
复数的加法与指数表达之间的等效换算关系如图 3 所示,关于更多更全面的复数计算及复变函数介绍请参考专门的复数教科书[1],在这里需要指出的一点是,有些作者可能是图省事,在实部虚部求幅角的时候简单但错误地表达成 b/a 的反正切,这种简单不仅错在 a 的数值为0时非常尴尬,更在于反正切的函数范围只在第一与第四象限,当复数位于第二或第三象限时将不可避免地出现往第一第四象限折叠的问题。正确的做法是对实部、虚部的符号做分类处理,即需要双参数输入函数,在多种编程语言中已经有现成的函数模块可供调用,比如脚本语言中一般支持 atan2 函数,它支持双参数输入并能输出完整四象限角度,图形语言比如 labview中直接有实部虚部到幅度幅角的转换函数。还有一点值得一提,虽然实部虚部与极坐标表示之间能够相互换算,但严格来讲二者并不完全等价。关键在原点处,实部虚部定义0 i0很自然,不过极坐标表示就没有确定的相位角,尽管编程语言中通常将原点的相位角置零,运用的人要清楚这个细微但却是本质的差异。不管怎样,读者看过本文以后如再碰到文章或教科书中直接将 b/a 的反正切作为复数的相位角,完全有理由直接怀疑其作者对复数的理解与认知水平。
图2 复数构成的代数与几何图示
复数的加法与指数表达之间的等效换算关系如图 3 所示,关于更多更全面的复数计算及复变函数介绍请参考专门的复数教科书[1],在这里需要指出的一点是,有些作者可能是图省事,在实部虚部求幅角的时候简单但错误地表达成 b/a 的反正切,这种简单不仅错在 a 的数值为0时非常尴尬,更在于反正切的函数范围只在第一与第四象限,当复数位于第二或第三象限时将不可避免地出现往第一第四象限折叠的问题。正确的做法是对实部、虚部的符号做分类处理,即需要双参数输入函数,在多种编程语言中已经有现成的函数模块可供调用,比如脚本语言中一般支持 atan2 函数,它支持双参数输入并能输出完整四象限角度,图形语言比如 labview中直接有实部虚部到幅度幅角的转换函数。还有一点值得一提,虽然实部虚部与极坐标表示之间能够相互换算,但严格来讲二者并不完全等价。关键在原点处,实部虚部定义0 i0很自然,不过极坐标表示就没有确定的相位角,尽管编程语言中通常将原点的相位角置零,运用的人要清楚这个细微但却是本质的差异。不管怎样,读者看过本文以后如再碰到文章或教科书中直接将 b/a 的反正切作为复数的相位角,完全有理由直接怀疑其作者对复数的理解与认知水平。
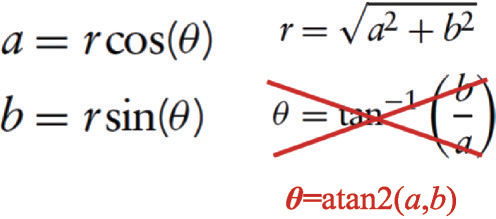 图 3 复数的两种基本表示方法之间的等价换算
实数运算拓展到复数运算因为产生新的现象,不能完全受实数运算中的规则束缚,有些在实数中的常识,在复数运算处理时可能并不适用要引起注意,这里举例讲复数乘方运算中的一条反常识之处:复数乘方运算稍不注意就会引起自相矛盾的悖论,如图4所示,据记载最初由放牛娃出身的克劳森(thomasclausen)于1827年提出[2]。克劳森悖论实际上不是复数的问题,而是在复数乘方运算过程中,复底数的相位求取是多值化的,跟乘方运算的指数相乘的相位应当为相位主值加上2πk (k 为整数)。如图5所示的两个乘方运算结果举例,ii 等于一系列实数,其中k=0时相位主值对应的值为 e(- π/2),一个约等于0.2的无理数;另一个例子,1i 根据实数乘方运算常识,1的所有次方总等于1,但这里1只是其结果之一,因为 1i 除了在k=0时等于1以外,还对应其他无穷个结果。当然,复数运算中也有人类迄今尚未理解的难题,比如让人着迷却仍然不得其解的黎曼猜想,由于已经超过本文的讨论范围,感兴趣的读者请自己去检索。
图 3 复数的两种基本表示方法之间的等价换算
实数运算拓展到复数运算因为产生新的现象,不能完全受实数运算中的规则束缚,有些在实数中的常识,在复数运算处理时可能并不适用要引起注意,这里举例讲复数乘方运算中的一条反常识之处:复数乘方运算稍不注意就会引起自相矛盾的悖论,如图4所示,据记载最初由放牛娃出身的克劳森(thomasclausen)于1827年提出[2]。克劳森悖论实际上不是复数的问题,而是在复数乘方运算过程中,复底数的相位求取是多值化的,跟乘方运算的指数相乘的相位应当为相位主值加上2πk (k 为整数)。如图5所示的两个乘方运算结果举例,ii 等于一系列实数,其中k=0时相位主值对应的值为 e(- π/2),一个约等于0.2的无理数;另一个例子,1i 根据实数乘方运算常识,1的所有次方总等于1,但这里1只是其结果之一,因为 1i 除了在k=0时等于1以外,还对应其他无穷个结果。当然,复数运算中也有人类迄今尚未理解的难题,比如让人着迷却仍然不得其解的黎曼猜想,由于已经超过本文的讨论范围,感兴趣的读者请自己去检索。
 图4 克劳森提出的复指数悖论问题[2]
图4 克劳森提出的复指数悖论问题[2]
 图5 虚指数的多值性示例
至此,复数的基本概念及运算规则已经介绍结束。然而,不得不承认,复数是怎样被发展出来的,前面的介绍只是过于简单的版本,跟真实的人类认识与应用复数的历史出入比较大,如果要我对于历史这段不严谨的介绍给一个借口,那无非是为了节约读者的宝贵时间,而且这个介绍丝毫不影响复数是什么这一知识的获取。如果只重知识,不管真实,可以跳过本段去直接阅读下一章。但凡是对真实有点兴趣的读者,建议耐心看完本段文字与汇总本段的图6。笔者认为,知道真实的知识产生的过程,不仅仅能让我们珍惜自己轻松就学到的知识,也让我们意识到我们学到的知识并非人类知识的终点,进而让自己的内心被薪火相传,并获得进一步去创新从而延伸人类知识的动力。如图6所示,这是一个以千年的 时 间 尺 度 通 过 关 键 事 件 节 点 (what/when/who) 依次串联来描述我们人类认识与应用复数的过程,事件涉及到的时间与人物的原始数据部分来源于nahin博士的书与数学手册[2,3],为了读者能更好地理解这个进展过程,笔者将这些事件分成几类进行介绍:
图5 虚指数的多值性示例
至此,复数的基本概念及运算规则已经介绍结束。然而,不得不承认,复数是怎样被发展出来的,前面的介绍只是过于简单的版本,跟真实的人类认识与应用复数的历史出入比较大,如果要我对于历史这段不严谨的介绍给一个借口,那无非是为了节约读者的宝贵时间,而且这个介绍丝毫不影响复数是什么这一知识的获取。如果只重知识,不管真实,可以跳过本段去直接阅读下一章。但凡是对真实有点兴趣的读者,建议耐心看完本段文字与汇总本段的图6。笔者认为,知道真实的知识产生的过程,不仅仅能让我们珍惜自己轻松就学到的知识,也让我们意识到我们学到的知识并非人类知识的终点,进而让自己的内心被薪火相传,并获得进一步去创新从而延伸人类知识的动力。如图6所示,这是一个以千年的 时 间 尺 度 通 过 关 键 事 件 节 点 (what/when/who) 依次串联来描述我们人类认识与应用复数的过程,事件涉及到的时间与人物的原始数据部分来源于nahin博士的书与数学手册[2,3],为了读者能更好地理解这个进展过程,笔者将这些事件分成几类进行介绍:
 图6 以千年尺度汇总显示人类认识与应用复数的历史进程
(1) 奠基
复数的最初渊源从代数与几何的方向分别可追溯到公元300年由丢番图(diophantus)整理编写的《arithmetica》(算术),与公元888年由欧几里得 (euclid) 编写的《elements》(几何原本)。
(2) 铺垫
1545年卡尔达诺 (cardano) 在《ars magna》(大衍术)中系统进行了负数及运算的论述,首次公开负数的平方根数的概念;1637年笛卡尔(descartes)在《la geometrie》(几何学)中公开了 a ib 解析法处理复数;韦塞尔(wessel)于1797年公开虚实轴组成复平面处理矢量的思想;柯西(cauchy)在1814年公开复函数可微条件,拉开了复变函数的微积分学;洛朗(laurent)于1843年公开了复变函数独有的一套级数思想与零点和极点处理方法,引入留数(洛朗级数的一次倒数项系数);1807 年傅里叶(fourier)公开倍频但幅度稳定的正弦余弦分别作为虚部实部的级数来进行函数的分解;1785年拉普拉斯(laplace)引入一套复指数变换方法,研究失稳过程有时非它不可。
(3) 点睛
前面提过的欧拉恒等式由欧拉(euler)在1748年公开证明,没有欧拉,这个恒等式也许会被引入,但不知道要迟多少年;一向谨慎低调的数学王子高斯(gauss)在1813年终于公开确立复平面的历史地位,复数的全面推广从此正式开始;闵可夫斯基(minkowski)于1907年公布通过虚数单位和光速跟时间相乘,三维空间复合,引入四维时空,证明了时空相对变化中的绝对不变;薛定谔(schrödinger)在1926年提出闻名于世的电子波动力学方程,尽管原文 phys. rev., 28, 1049(1926)中没有直白地写出他去世后在墓碑上刻着带虚数单位模样的方程(如图6中1926年事件块中所列),但在原文第9部分对含时波函数中出现虚数单位与相位±2πet/h,足够表达波函数在特定能量下的振荡性质,并启发后人理解量子力学的奥妙。
(4) 发扬
首先不得不提黎曼(riemann),尽管40岁就英年早逝,但在他短暂的一生中,除了前面提到的黎曼猜想,他与柯西一样都对复分析作出了重要贡献,而且比柯西更加富有创造性地从微分几何角度开展复分析,并首次往人类数理知识库中引入非欧几何,这对20世纪广义相对论与弦论的诞生提供了良好的铺垫。
狄拉克(dirac)对量子力学波函数进行了相对论性改造,其中关键的一步是将哈密顿算符变成4×4的复矩阵,利用矩阵具有反对易性质调和了时间与空间平方反对称与一阶微分对等之间的矛盾,让经过改造后的波函数的第四分量非常好地对应解释电子1/2自旋,并预言了正电子的存在,极大地推动了量子力学的发展。
外尔(weyl)在统一电磁场与引力场,构建伟大的规范不变理论的过程中,至关重要的一步是,找到跟电荷守恒相对应的对称性是复波函数的相位不变性,该相位不变规律在电磁学中可以推导出麦克斯韦方程组,是电磁相互作用理论的终极基石。
杨振宁(c. n. yang)经过艰苦卓绝的群论推演,用2×2复矩阵找到质子与中子之间的同位旋对称,后来盖尔曼(murray gell-mann)经过3×3的复矩阵运算进一步获知微观世界基本粒子的构建规则,从而准确解释或预测出全部微观基本粒子的种类及相互作用,杨先生与盖尔曼引入被称为标准模型的理论实现了除引力外所有已知基本力的伟大统一。顺便一提,在2000年杨先生回顾20世纪物理学三大主旋律为:量子、对称、相位因子。
(5) 遗憾
在复数的发展过程中,从二元复数到多元复矩阵的过程中,代数学上还经历过三元数、四元数、乃至八元数的尝试,其中最著名的要数哈密顿(hamilton)创立的四元数(quaternion),遗憾的是,多元复数的代数运算简洁程度与效果比不上2×2与4×4复矩阵,从而在20世纪物理学发展的大舞台上并没有获得哈密顿本人预期的实用,尽管在比较小的学科分支上也有独到的应用,比如将四元数的模设成1时可以用于描述三维空间旋转,空间导航时相比通常的欧拉角方法有更小的误差与较高稳定性。当然,形式上将 lijk 换成2×2复矩阵组并不影响实质上的大同小异,从这个意义上讲,形式上未被重视不应该掩盖哈密顿的超复数思想与逻辑的伟大。
除此以外,19世纪中叶,复数的概念已经被数学主流认可并应用的时候,逻辑代数创始人布尔(boole)却坚持认为虚数单位是不可解释的符号,现在看来让人难以理解,不过二值比特逻辑有其自身的优势及发展之路,虚数在数值逻辑中的确不必要,或许在未来某天模拟计算与数值计算平分秋色之时,复数在计算机架构中的重要性将不言而喻。
还有,麦克斯韦(maxwell)在他1865年“a dynamic-al theory of theelectromagnetic field”论文中,未见使用虚数,子方程数达20个之多, 后来多亏oliver heaviside与willard gibbs运用矢量分析进行大幅度改造才使得麦克斯韦方程组成型到容易理解的闻名于世的四个子方程形式,当然瑕不掩瑜,麦克斯韦的这篇论文在电磁规律综合并牢固确立场的概念、引入位移电流、同时通过波速证明电磁波是光这几个方面的贡献是划时代的。
(6) 插曲
我们知道,负数是虚数之源,虚数的引入必须以负数为前提,但不知因何原因,在古代中国引入并运用负数非常自然,而西方正式接受负数比中国晚约1700年,不过西方在接受负数后随即就开启了虚数的研究,而中国人对虚数的发展未见任何实质性的贡献,只是由《数书九章》中秦九韶提出的二次、三次及高次方程求解算法,可见他是中国古人中距离虚数发现最近的人,而且更加难能可贵的是,《数书九章》是《几何原本》与《大衍术》之间约600年间地球上数一的数学著作。
还有一则,在欧拉恒等式被引入之前,复数的计算通常需要高超的数学技巧,比如约翰·伯努利运用(x i)(x-i)=1 x 2 的技巧找到了反正切与对数函数之间的内在联系,并运用于虚数因子分解积分,被莱布尼茨(leibniz)评价为非凡智能的一个优美神奇。
(7) 可期
跟其他人类知识体系一样,复数发展至今不应是终点,未来有更重要的发展事件也是可期的。我们知道以复数波函数为主要特征的量子力学样样都好,屡次都被证明是正确的,至今也还没有发现被实验结果证否的事件,但就是推不出引力方程,让人隐忧哪里有些不对,实现大统一或证明大统一是不可能实现的幻想的突破性的事件,让我们努力使它在我们有生之年发生。
图6 以千年尺度汇总显示人类认识与应用复数的历史进程
(1) 奠基
复数的最初渊源从代数与几何的方向分别可追溯到公元300年由丢番图(diophantus)整理编写的《arithmetica》(算术),与公元888年由欧几里得 (euclid) 编写的《elements》(几何原本)。
(2) 铺垫
1545年卡尔达诺 (cardano) 在《ars magna》(大衍术)中系统进行了负数及运算的论述,首次公开负数的平方根数的概念;1637年笛卡尔(descartes)在《la geometrie》(几何学)中公开了 a ib 解析法处理复数;韦塞尔(wessel)于1797年公开虚实轴组成复平面处理矢量的思想;柯西(cauchy)在1814年公开复函数可微条件,拉开了复变函数的微积分学;洛朗(laurent)于1843年公开了复变函数独有的一套级数思想与零点和极点处理方法,引入留数(洛朗级数的一次倒数项系数);1807 年傅里叶(fourier)公开倍频但幅度稳定的正弦余弦分别作为虚部实部的级数来进行函数的分解;1785年拉普拉斯(laplace)引入一套复指数变换方法,研究失稳过程有时非它不可。
(3) 点睛
前面提过的欧拉恒等式由欧拉(euler)在1748年公开证明,没有欧拉,这个恒等式也许会被引入,但不知道要迟多少年;一向谨慎低调的数学王子高斯(gauss)在1813年终于公开确立复平面的历史地位,复数的全面推广从此正式开始;闵可夫斯基(minkowski)于1907年公布通过虚数单位和光速跟时间相乘,三维空间复合,引入四维时空,证明了时空相对变化中的绝对不变;薛定谔(schrödinger)在1926年提出闻名于世的电子波动力学方程,尽管原文 phys. rev., 28, 1049(1926)中没有直白地写出他去世后在墓碑上刻着带虚数单位模样的方程(如图6中1926年事件块中所列),但在原文第9部分对含时波函数中出现虚数单位与相位±2πet/h,足够表达波函数在特定能量下的振荡性质,并启发后人理解量子力学的奥妙。
(4) 发扬
首先不得不提黎曼(riemann),尽管40岁就英年早逝,但在他短暂的一生中,除了前面提到的黎曼猜想,他与柯西一样都对复分析作出了重要贡献,而且比柯西更加富有创造性地从微分几何角度开展复分析,并首次往人类数理知识库中引入非欧几何,这对20世纪广义相对论与弦论的诞生提供了良好的铺垫。
狄拉克(dirac)对量子力学波函数进行了相对论性改造,其中关键的一步是将哈密顿算符变成4×4的复矩阵,利用矩阵具有反对易性质调和了时间与空间平方反对称与一阶微分对等之间的矛盾,让经过改造后的波函数的第四分量非常好地对应解释电子1/2自旋,并预言了正电子的存在,极大地推动了量子力学的发展。
外尔(weyl)在统一电磁场与引力场,构建伟大的规范不变理论的过程中,至关重要的一步是,找到跟电荷守恒相对应的对称性是复波函数的相位不变性,该相位不变规律在电磁学中可以推导出麦克斯韦方程组,是电磁相互作用理论的终极基石。
杨振宁(c. n. yang)经过艰苦卓绝的群论推演,用2×2复矩阵找到质子与中子之间的同位旋对称,后来盖尔曼(murray gell-mann)经过3×3的复矩阵运算进一步获知微观世界基本粒子的构建规则,从而准确解释或预测出全部微观基本粒子的种类及相互作用,杨先生与盖尔曼引入被称为标准模型的理论实现了除引力外所有已知基本力的伟大统一。顺便一提,在2000年杨先生回顾20世纪物理学三大主旋律为:量子、对称、相位因子。
(5) 遗憾
在复数的发展过程中,从二元复数到多元复矩阵的过程中,代数学上还经历过三元数、四元数、乃至八元数的尝试,其中最著名的要数哈密顿(hamilton)创立的四元数(quaternion),遗憾的是,多元复数的代数运算简洁程度与效果比不上2×2与4×4复矩阵,从而在20世纪物理学发展的大舞台上并没有获得哈密顿本人预期的实用,尽管在比较小的学科分支上也有独到的应用,比如将四元数的模设成1时可以用于描述三维空间旋转,空间导航时相比通常的欧拉角方法有更小的误差与较高稳定性。当然,形式上将 lijk 换成2×2复矩阵组并不影响实质上的大同小异,从这个意义上讲,形式上未被重视不应该掩盖哈密顿的超复数思想与逻辑的伟大。
除此以外,19世纪中叶,复数的概念已经被数学主流认可并应用的时候,逻辑代数创始人布尔(boole)却坚持认为虚数单位是不可解释的符号,现在看来让人难以理解,不过二值比特逻辑有其自身的优势及发展之路,虚数在数值逻辑中的确不必要,或许在未来某天模拟计算与数值计算平分秋色之时,复数在计算机架构中的重要性将不言而喻。
还有,麦克斯韦(maxwell)在他1865年“a dynamic-al theory of theelectromagnetic field”论文中,未见使用虚数,子方程数达20个之多, 后来多亏oliver heaviside与willard gibbs运用矢量分析进行大幅度改造才使得麦克斯韦方程组成型到容易理解的闻名于世的四个子方程形式,当然瑕不掩瑜,麦克斯韦的这篇论文在电磁规律综合并牢固确立场的概念、引入位移电流、同时通过波速证明电磁波是光这几个方面的贡献是划时代的。
(6) 插曲
我们知道,负数是虚数之源,虚数的引入必须以负数为前提,但不知因何原因,在古代中国引入并运用负数非常自然,而西方正式接受负数比中国晚约1700年,不过西方在接受负数后随即就开启了虚数的研究,而中国人对虚数的发展未见任何实质性的贡献,只是由《数书九章》中秦九韶提出的二次、三次及高次方程求解算法,可见他是中国古人中距离虚数发现最近的人,而且更加难能可贵的是,《数书九章》是《几何原本》与《大衍术》之间约600年间地球上数一的数学著作。
还有一则,在欧拉恒等式被引入之前,复数的计算通常需要高超的数学技巧,比如约翰·伯努利运用(x i)(x-i)=1 x 2 的技巧找到了反正切与对数函数之间的内在联系,并运用于虚数因子分解积分,被莱布尼茨(leibniz)评价为非凡智能的一个优美神奇。
(7) 可期
跟其他人类知识体系一样,复数发展至今不应是终点,未来有更重要的发展事件也是可期的。我们知道以复数波函数为主要特征的量子力学样样都好,屡次都被证明是正确的,至今也还没有发现被实验结果证否的事件,但就是推不出引力方程,让人隐忧哪里有些不对,实现大统一或证明大统一是不可能实现的幻想的突破性的事件,让我们努力使它在我们有生之年发生。
 图7 锁相放大器测量原理示意图[4]
由测量原理看出ω0频点的稳定极为重要,在普通的振荡源的频率稳定性不够的时候,需要增加锁相环(phase lock loop,pll)部件,其结构如图8所示,在强制外部参考的模式下,受控振荡源为了和外部频点保持一致,需要实时测量跟外部参考信号的相位差并进行自我调整,通过相位差的锁定来维持测量频点的稳定。因而这种复数测量方法与工具通常被称之为锁相技术与锁相放大器(lock in amplifiers)。
图7 锁相放大器测量原理示意图[4]
由测量原理看出ω0频点的稳定极为重要,在普通的振荡源的频率稳定性不够的时候,需要增加锁相环(phase lock loop,pll)部件,其结构如图8所示,在强制外部参考的模式下,受控振荡源为了和外部频点保持一致,需要实时测量跟外部参考信号的相位差并进行自我调整,通过相位差的锁定来维持测量频点的稳定。因而这种复数测量方法与工具通常被称之为锁相技术与锁相放大器(lock in amplifiers)。
 图8 锁相环结构图示[4]
如此可见,用锁相技术实现复数测量的关键在于交流变化维度的锁相环跟踪与实部虚部的正交相敏检波测量,更多的专业介绍请参考文献[4]。这里对锁相的含义,为让外行人能更好理解这个复数测量的强大工具,做一点延伸解读:锁相,跟成语相夫教子中的作为动词的“相”含义默契,夫妇之间的关系实际上是一个长期的相位和步调通过锁定达到美满的境界,如果失锁就比较麻烦了。此外,锁相环这种自动保持稳定步调但又具备一定的随外界环境而自我调节能力的神奇部件,何尝不是一个原始态的机器心灵?
图8 锁相环结构图示[4]
如此可见,用锁相技术实现复数测量的关键在于交流变化维度的锁相环跟踪与实部虚部的正交相敏检波测量,更多的专业介绍请参考文献[4]。这里对锁相的含义,为让外行人能更好理解这个复数测量的强大工具,做一点延伸解读:锁相,跟成语相夫教子中的作为动词的“相”含义默契,夫妇之间的关系实际上是一个长期的相位和步调通过锁定达到美满的境界,如果失锁就比较麻烦了。此外,锁相环这种自动保持稳定步调但又具备一定的随外界环境而自我调节能力的神奇部件,何尝不是一个原始态的机器心灵?
 图9 频率、幅度和相位之间一体性关系的图示
图9 频率、幅度和相位之间一体性关系的图示




 图14 极微观结构与超宏观事件探测都离不开复数测量(显微探针与引力波探测示意图均源自网络)
随着中国智造的加速转型,复数测量的普适度与深度在继续,在人类看得见摸得着的范围内,未来的智能感知、准确定位与互联、精密制造、与痕量物质探测中锁相测量的应用前景让人乐观。在人类肉眼难以感知到的超微观与超宏观世界,如图14所示,亚原子与深太空探索更是无止境,无论浩瀚与微渺,不管刹那还是永恒:复数事件不息,复数测量不止。
图14 极微观结构与超宏观事件探测都离不开复数测量(显微探针与引力波探测示意图均源自网络)
随着中国智造的加速转型,复数测量的普适度与深度在继续,在人类看得见摸得着的范围内,未来的智能感知、准确定位与互联、精密制造、与痕量物质探测中锁相测量的应用前景让人乐观。在人类肉眼难以感知到的超微观与超宏观世界,如图14所示,亚原子与深太空探索更是无止境,无论浩瀚与微渺,不管刹那还是永恒:复数事件不息,复数测量不止。



