翻译: 方正michael 后期: 公理 英文: https://sourl.cn/eycdtv
有时候,人类科学的发展需要超越传统的思维方式。
在 20 世纪早期,物理学上的两次革命——爱因斯坦的相对论(首先是狭义的,然后是广义的)和量子力学——带来了对数学的需求,而所需要的工具仅用实数是满足不了的。从那时起,由实部和虚部组成的复数就与我们对宇宙的理解不可分割地纠缠在一起。
从数学上讲,当我们想到数字时,可以想到几种不同的分类方法:
可数数字:1、2、3、4、…等。这样的数字有无数个。 自然数:0、1、2、3、…等。这些数与可数数相同,但同时包括零。 整数:...,-3, -2, -1, 0, 1, 2, 3, ...等。这看起来可能不多,但认识到我们可以有负数是一个巨大的突破,而且负数和正数一样多。整数包括所有的自然数和它们的负数。 有理数:可以表示为一个整数除以另一个整数的任何数字。这包括所有的整数(可以表示为它们本身除以 1)以及每个整数之间无穷多的有理数。任何无限循环的小数都可以用有理数来表示。 实数:包括所有的有理数以及所有的无理数,比如非完全平方的平方根,,以及其他的无理数。任何有理数和任何无理数的和都是无理数,但两个无理数的和可能是有理数。
但是,尽管正数的平方根是实数,负数的平方根却没有明确的定义。至少,它还未被定义,直到数学家并发明了虚数来进行定义!
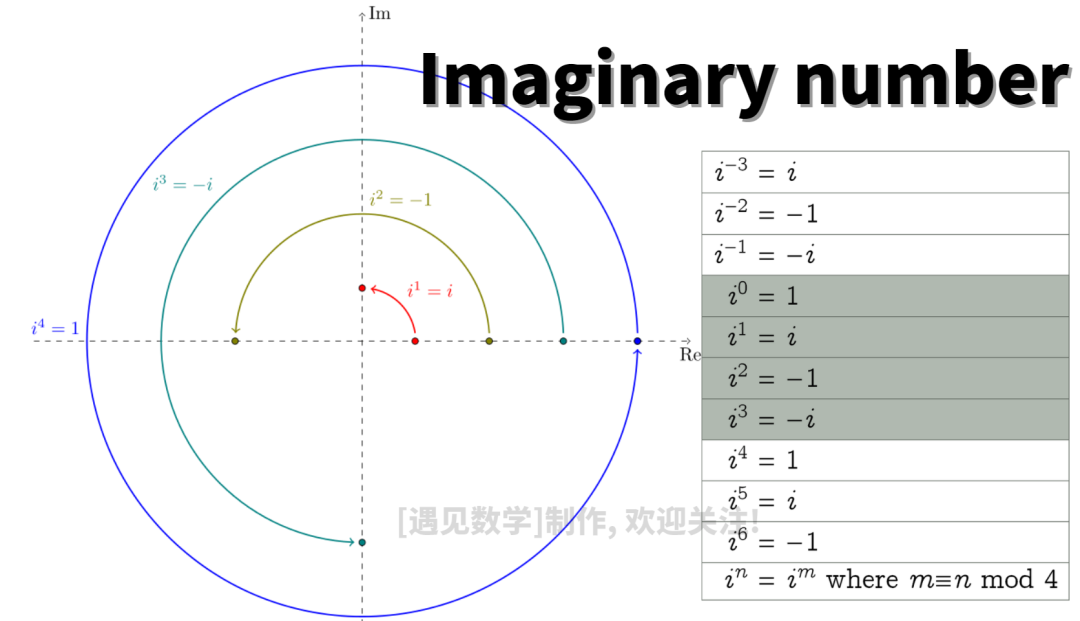
虚数和实数没什么两样,不过是实数概念的延伸,有个虚数单位i,或者说跟号-1。任一复数其中既有实部(a)也有虚部(b),通常用(a bi)表示,复数直接同样可以进行加减乘除,总而言之,复数系统是一个域。
现在你知道它们是什么了,下面5个是我认为关于虚数最有趣的事实!
一个负实数的平方根是纯虚数,但一个纯虚数的平方根必须同时有实部和虚部!下面是证明的方法。你需要某个数的平方等于跟号-1。假设它有一个实部x和一个虚部y,所以我们可以把它写成(x yi),然后我们可以算出x和y的值是多少。
两边同时平方
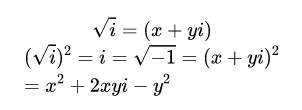
现在我们让实部与实部对应,虚部与虚部对应。
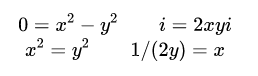
通过这两个方程,我们可以把右边方程的x代入左边方程,
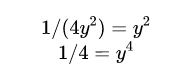
然后,我们便可以解出y:
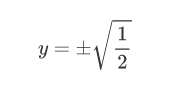
如你所见,有两种可能的解,如果我们用方程的右边(虚部)来解x(两种情况下y的值都一样),我们得到两个解:
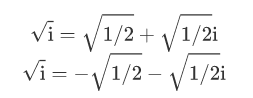
这就引出了下一个有趣的事实…
对于正实数,开方(即,第二个根)会给出两种可能的解:正的和负的。例如,跟号1可以是 1,也可以是-1,因为任意一个解的平方都是1。
但对于 i,也就是 ,如果你想求根,你需要做一个多项式方程,就像我们上面做的那样。问题是,多项式方程的阶取决于我们取它的根。所以 的三、四、五次方根必须满足:
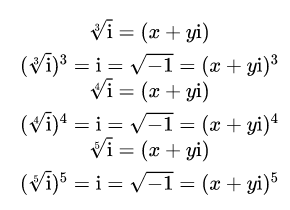
所以对于方程中的每一个x和y都有3个,4个,5个不同的解。例如, 的三次方根的三个解为:
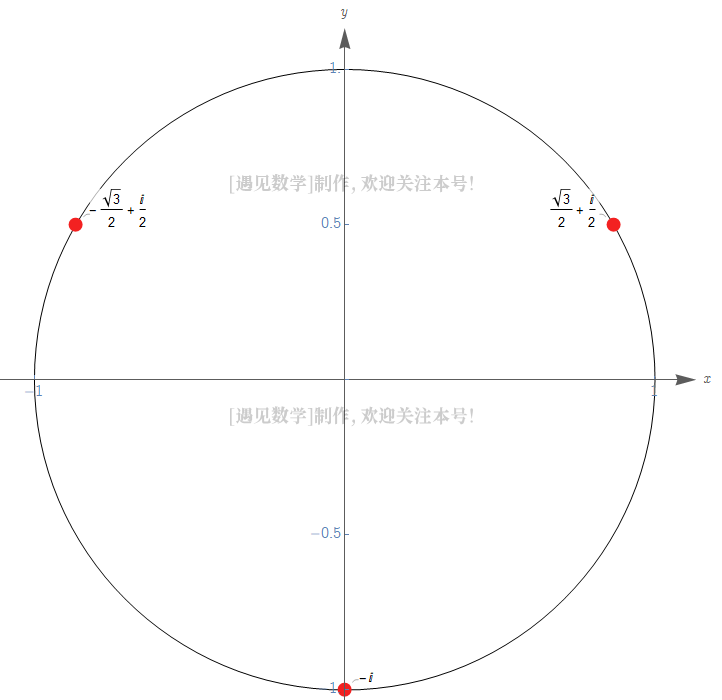
(尝试把它们立方,然后自己动手尝试下吧!)这甚至还没有涉及更复杂点的分数,请继续往下看……
在虚数分数中,i究竟是在分子中还是分母中是很重要的。如果你考虑(-1)这个数,在分数形式的情况下,不管你是用-1/1还是1/(-1) 来考虑它,其结果都是(-1)。但对i来说事实并非如此!我来问你们,你们认为这个分数是多少?
看着它,你可能认为它等于i,但实际上它是-i!
想要证明吗?只要分数上下同时乘以一个i,然后看吧
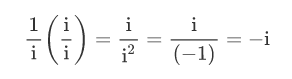
所以当对复数分数进行合并或分解时要小心谨慎,必须遵循一些复杂的规则才能得到正确的结果。违反它们,你可以做各种疯狂的事情,比如证明 1=-1,这样数学上称之为无效的证明。
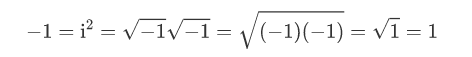
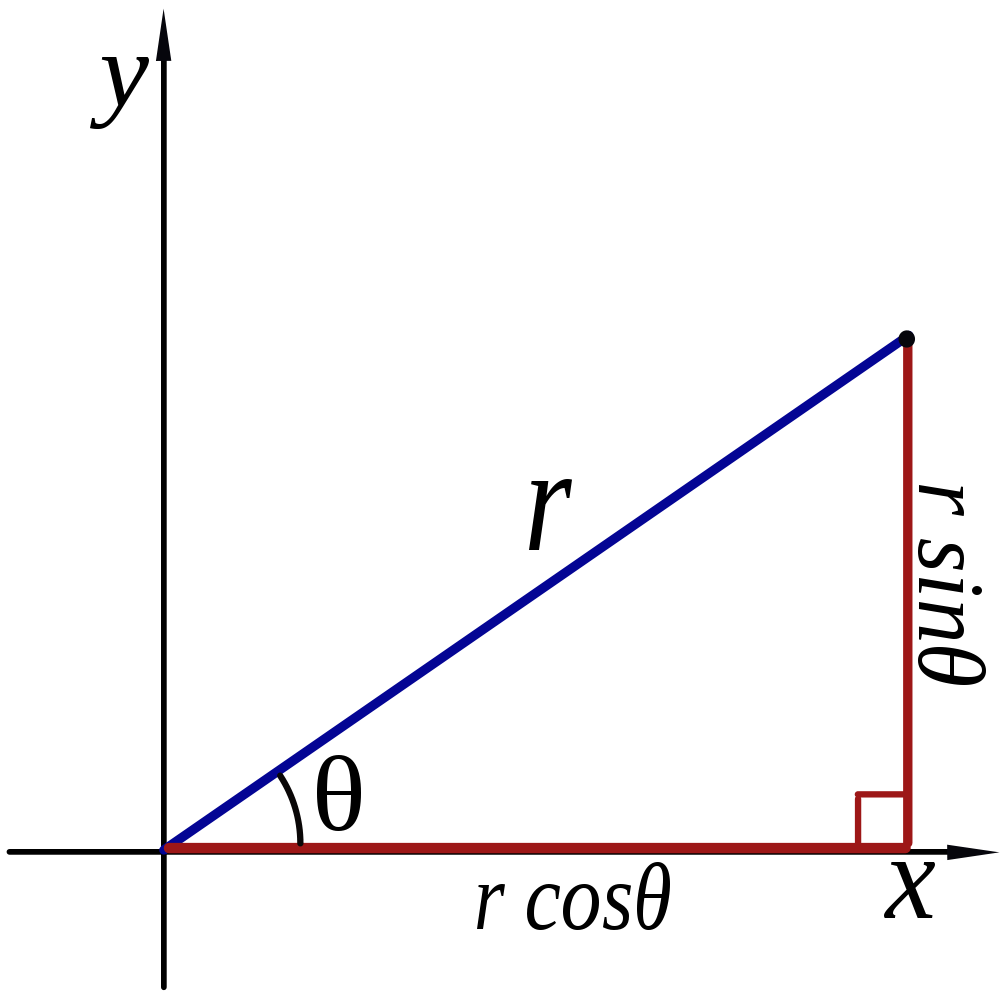
在数学中,我们可以用极坐标来表示二维坐标空间,其中有一个距离原点的径向坐标(r)和一个极角(θ),就像下图所示这样:
如果你不用x轴和y轴,而是用复平面(complex plane)中水平的实轴与垂直的虚轴建立起来的几何表示,这样也可以解释复数,只不过角度θ可以带你在实平面与虚平面之间转换,比如利用下面图形中的欧拉公式:
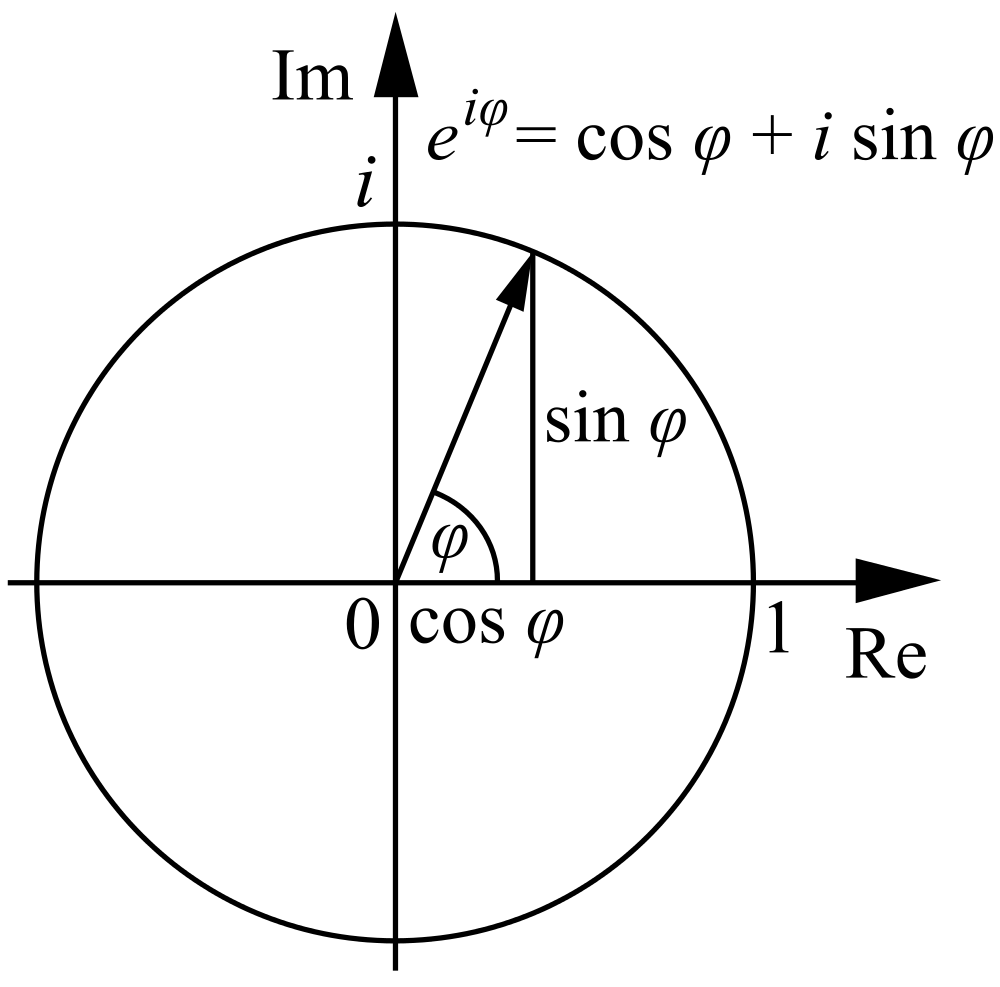
令人惊奇的是,如果我们在实轴上定位到-1的位置,会得到一个漂亮的恒等式,如下面的欧拉恒等式:
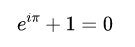
利用证明如下:

上面的欧拉公式会在复分析中经常出现,因为它把三角函数与复指数函数联系起来。现在看最后一个事实,也是很有意思的。
i的i次方是 100% 的实数。考虑上图中的方程(欧拉公式)——但我们不是在实轴上指向(-1)而是在虚轴上指向i。在这种情况下,我们会得到一个等式:
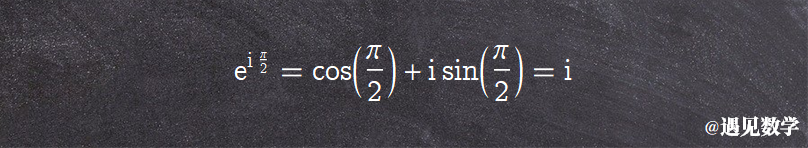
如果我们想知道i的i次方是多少,我们需要做的就是对等式两边同时取 次方,
记得i的平方等于-1吗,然后我们可以发现:
大概就是实数大概就是实数: ...
(- end -)

